Ezeken a feladatokon múlhatott a kettes

Koren Balázs matematikatanárral átnéztük azt a három feladatot, amin akár a kettes is múlhatott. Vagy éppen az ötös. Elsőre könnyűnek tűnő, de sokak által elrontható feladatokat mutatunk az elmúlt évek egyik legnehezebb matekérettségijéből. 

Az a bűvös harmadik feladat - minden szekrény barna?

Ötödik feladat - minden kocka testátlója 45 fokos szöget zár be az alappal?

Két dobókockával a dobott értékek szorzata mekkora valószínűséggel lesz prím szám? Íme a tizenkettedik feladat

Akár ezeken a feladatokon is múlhatott, hogy valakinek meglegyen a kettes vagy éppen az ötös az összesen 18 feladatból. A matekérettségi feladataiból 17-et kellett kötelezően megcsinálni. Nem mindet oldottuk meg, Koren Balázs matematikatanár segítségével a tanulságosabb és érdekesebb feladatokat mutatjuk be. Hangsúlyozzuk, hogy ez nem a hivatalos megoldókulcs, a feladatok levezetése különbözhetett. Íme tehát néhány érdekesebb feladat megoldása a matekérettségi első részéből.

Logikára épített például a hármas feladat, ami zavarba hozhatta a vizsgázókat.

3. Minden szekrény barna. Válassza ki az alábbiak közül annak a mondatnak a betűjelét, amely tagadása a fenti kijelentésnek.

A, Van olyan szekrény, ami nem barna.
B. Nincs barna szekrény
C. Van olyan szekrény, ami barna
D. Pontosan egy szekrény barna

A kérdésben lévő állítás akkor nem teljesül, ha tudok legalább egy olyan szekrényt találni, amely nem barna. Azaz: úgy tudom tagadni, ha azt mondom, hogy van olyan szekrény, amelyik nem barna. Ennek a betűjele pedig az A, így itt ez volt a jó megoldás.

Koren Balázs matematikatanár segített a példák megértésében Forrás: Origo

Érdekes és tanulságos volt az ötös feladat is, ami igaz és hamis állításokra kérdezett rá, ezeket pedig a megfelelő helyre kellett beírni.

5. Adja meg az alábbi állítások logikai értékét. (Igaz vagy hamis.)

A. Minden paralelogramma tengelyesen szimmetrikus négyszög.
Megoldás: HAMIS. Ezt minden bizonnyal a többség meg tudta oldani, hiszen van rá több ellenpélda is.
B. A kocka testátlója 45 fokos szöget zár be az alaplappal.
Megoldás: HAMIS. Ez már egy érdekesebb feladat, hiszen elsőre, gondolkodás nélkül sokan elhibázzák. Figyelni kellett rá ugyanis, hogy a négyzet esetében ugyan igaz az analóg állítás, de a kocka esetében nem.
C. A szabályos tizenhétszögben az egyik csúcsból kiinduló összes átló a tizenhétszöget 15 háromszögre bontja.
Megoldás: IGAZ. Ennél a feladatnál egyszerűen azt kell megnéznünk, hogy hány átló húzható a tizenhétszög csúcsából, ami a függvénytáblázatban is benne van: n-3. Tehát a tizenhétszög esetében 14 átlót fogunk tudni behúzni, ami összességében 15 háromszögre bontja fel azt.

12. Két különböző színű szabályos dobókockával egyszerre dobunk. Adja meg annak a valószínűségét, hogy a dobott számok szorzata prímszám lesz.

Fontos, hogy ennél a kérdésnél nem elegendő csak a választ megadnunk, hanem le kell írnunk a levezetést is. A levezetésre 3 pont jár, 1 pontot kapunk a helyes megoldásért. (Utóbbit egyébként sokan el szokták felejteni beírni a megfelelő helyre.)

Amikor két különböző dobókockával dobunk, a legegyszerűbb megoldás, ha készítünk egy lehetséges kimenettáblázatot. Fent az egyik, oldalt a másik dobókocka számai, így már rögtön látjuk, hogy a dobásoknak 36 féle kimenete lehet. Mivel mindkét kocka külön-külön mind a hat oldalára egyforma valószínűséggel fordulhat, a 36 kimenetel valószínűsége egyenlő.

Most nézzük meg, milyen prímszámokat kaphatunk a két dobókockával dobva: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31. Persze nem lepődünk meg azon, hogy csak az első sorban és az első oszlopban találunk prímeket, hiszen ha egytől különböző számokat szorzunk össze, az eredmény nem lehet prím.

Vizsgáljuk meg, mik azok a számok, amik meg is jelennek a táblázatban!

Ilyen táblázattal is meg lehetett oldani a feladatot Forrás: Origo

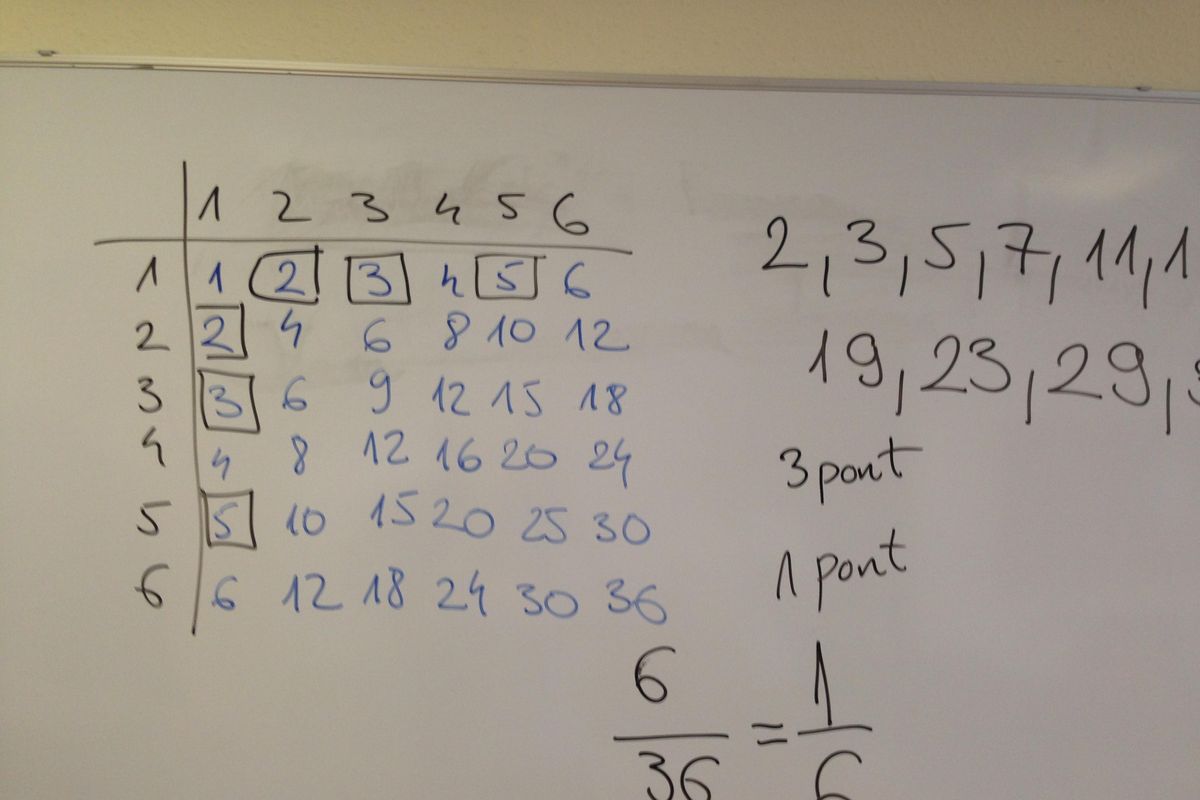
Összeszámolva hat darab ilyen érték lehetséges, azaz a keresett valószínűség a 6/36. A válaszunk tehát egyszerűsítve: 1/6-od.

Hamarosan jelentkezünk az érettségi második részének feladataival is. Koren Balázs videón magyarázza majd el a tanulságosabb megoldásokat.