Korszakalkotó égi mechanikai eredmény született az ELTE-n

Az ELTE TTK Földrajz- és Földtudományi Intézet Csillagászati Tanszékének kutatói – Érdi Bálint professzor emeritus és Czirják Zalán doktorandusz – Newton és Lagrange kétszáz esztendőnél is régebbi eredményei után először találtak explicit, egzakt analitikus megoldást a csillagászat és az űrkutatás egy központi jelentőségű kérdése, az égi mechanikai n-test probléma egy alosztályára.

A Nature is méltatja a magyar kutatók eredményét

Az áttörést két rendkívül eredeti ötlet tette lehetővé, a számítás azonban még így is nagyon összetett: a levezetéseket teljes részletességgel ismertető kézirat terjedelme 57 oldal, az eredményeket a szakmai nyilvánosság előtt bemutató, a Celestial Mechanics and Dynamical Astronomy folyóiratban megjelent publikációé pedig 38 oldal. A világ vezető természettudományos folyóirata, a Nature 2016. május 12-i számában meghívott szerkesztőségi cikkben méltatja Érdi Bálint és Czirják Zalán eredményét.

A 18. századra datálódik az égi mechanikai feladvány

Az n darab, csak gravitációsan kölcsönható, pontszerűnek tekintett test mozgását vizsgáló n-testprobléma a csillagászat és űrkutatás központi jelentőségű kérdése, hiszen döntő szerepe van az égitestek és a mesterséges űreszközök pályájának meghatározásában.

Az n-testprobléma az égitestek és űreszközök pályájának meghatározásában lényeges kérdés Forrás: NASA/JPL

Bár a kéttest-probléma általános megoldását már Newton megadta (ennek tulajdonságait összegzik a bolygómozgás jól ismert Kepler-féle törvényei), 2-nél nagyobb n értékek esetére általános megoldás nem létezik.

Forrás: ELTE

A háromtest-probléma megoldásainak egy alosztályát, az ún. centrális konfigurációkat Euler és Lagrange határozták meg analitikusan a 18. században. Ezek közül a Lagrange-féle megoldásoknak léteznek kézenfekvő általánosításai több test esetére is: 4 test esetében ezek tetraéder alakú konfigurációkat jelentenek.

Joseph Louis Lagrange francia származású 18. századi olasz matematikus és csillagász Forrás: Wikimedia Commons

További egzakt, explicit analitikus megoldások azonban nem születtek az n-test problémára –

egészen Érdi Bálint és Czirják Zalán új eredményeiig,

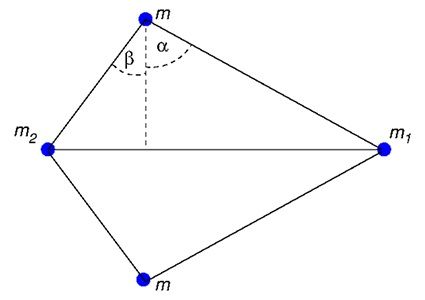
melyekben a síkbeli, szimmetrikus négytest-probléma centrális konfigurációira (olyan elrendezés, ahol a testekre ható erő a rendszer tömegközéppontjába mutat) adnak teljes, egzakt és explicit analitikus megoldást. A síkbeli, szimmetrikus négytest-probléma deltoid alakú konfigurációkat jelent, ahol a deltoid avagy sárkány-alakzat „szárnyait” alkotó két test tömege azonos.

Még általánosabb megoldásokhoz nyitották ki az ajtót

Az új megoldásokat lehetővé tevő ötletek egyike abban áll, hogy a kutatók a hagyományos, pl. Descartes-féle vagy polárkoordináták alkalmazása helyett, az ábrán α-val és β-val jelölt szögekkel paraméterezik a vizsgált konfigurációkat. Másrészt, eltérően a szokásos megközelítési módtól, ahol a testek tömegét rögzítve keresik a mozgás során alakjukat megőrző centrális konfigurációkat,

az ELTE kutatói az inverz problémát oldották meg:

adott konfigurációhoz keresték meg azokat a tömegarányokat, amelyek mellett a centrális konfiguráció fennmarad.

Johannes Kepler 17. századi német csillagász, a bolygómozgások három alapvető égi mechanikai törvényének megalkotója Forrás: Wikimedia Commons

Az új eredmény speciális esetekként visszaadja a háromtest-probléma korábban ismert Lagrange-megoldásait, valamint a négytest-probléma néhány korábban numerikus úton talált partikuláris megoldását. Ahogyan ez az új megoldás összefoglalja és kiterjeszti a korábban ismert részmegoldásokat, ugyanúgy lehetséges, hogy a jövőben azokhoz hasonlóan még általánosabb megoldások alapjául szolgálhat majd.

Még csak találgatni lehet az eredmény űrtechnikai jelentőségét

Az új elméleti eredmény potenciális gyakorlati alkalmazásainak lehetőségét egyelőre felmérni is alig tudjuk. Lagrange aligha sejtette, hogy a háromtest-probléma róla elnevezett librációs pontjaiba korunkban fix telepítésű űrobszervatóriumok kerülnek, vagy azt, hogy az ilyen pontokat a Naprendszerben összekapcsoló pályák hálózata, az ún. Bolygóközi Transzporthálózat a legkorszerűbb, ionmeghajtású űrszondák közlekedése segíti.

A Naprendszer bolygói Forrás: NASA/JPL

A négytest-probléma Érdi-Czirják-féle megoldásainak űrtechnikai felhasználását még csak találgatni lehet – elképzelhető például, hogy egy napon alakzatban repülő űrhajóflották valósítják meg az újonnan talált konfigurációkat az alakzat üzemanyagtakarékos fenntartása érdekében.

(Forrás: ELTE Földrajz – és Földtudományi Intézet Csillagászati Tanszéke)