Talán most valóra válik, ami nem sikerült Einsteinnek


Bár mind a relativitáselmélet, mind a kvantummechanika teóriája jól tesztelt elméletek, mégis összeférhetetlennek tűnnek egymással, és eddig még senkinek sem sikerült egyetlen átfogó elméletbe, egységbe foglalni a kettőt, még a 20. század leghíresebb elméleti fizikusának, Albert Einsteinnek sem.

Az általános relativitáselmélet tulajdonképpen maga is egyesítés.
Einstein rájött, hogy a tér és az idő egyazon dolognak, a téridőnek a különböző aspektusai. A nagy objektumok – mint például a csillagok – körül lévő tér szerkezete „meggyűrődik”, és eltorzítja a téridőt: a gravitáció e gyűrődés következménye, amely nem más, mint a tér és az idő görbülete.
Az általános relativitáselmélet jól tesztelt, eddig minden próbát kiállt, és előrejelzései pontosak voltak.
A hétköznapi életben sok helyütt alkalmazzák az általános relativitáselmélet következményeit, így többek között a traffipax vagy a GPS is lényegét tekintve a relativitáselméleten alapszik.

Ha nem számítanák be a relativisztikus hatásokat, egy GPS-egység, ami azt mutatja például, hogy a legközelebbi benzinkút 804,672 méterre van tőlünk, egy nappal később már azt mutatná, hogy ugyanez 8 kilométerre esik.

Az általános relativitáselmélet ott van az érzékeny műholdaktól kezdve a gravitációs lencséig, vagy a csillagok pályájától az óriási fekete lyukak körül kimutatott gravitációs hullámokig terjedően, egészen az univerzum evolúciójáig bezárólag.
A kvantummechanika szerint minél kisebb skálán nézzük a világot, annál véletlenszerűbbek az események.
Heisenberg határozatlansági relációja kimondja,
hogy az egymáshoz kanonikusan konjugált változók, mint például a hely és az impulzus, vagy az idő és az energia, nem mérhetők meg egyszerre tetszőleges pontossággal, és a mérési bizonytalanságok szorzata mindig nagyobb, mint ħ/2π. (Két mennyiség kanonikusan konjugált, ha egymás Fourier-transzformáltjai.)

Ennek következménye, hogy Heinsenberg-féle határozatlansági relációba kerülnek egymással, vagyis bizonytalanságaik (szórásaik) szorzata nem csökkenthető egy általános határ alá, amely a redukált Planck-állandó fele.
Az elektron és minden más részecske is hullámtulajdonságokat is mutat. Ez a kettős természet, a részecske-hullám természet az anyagnak általános tulajdonsága.
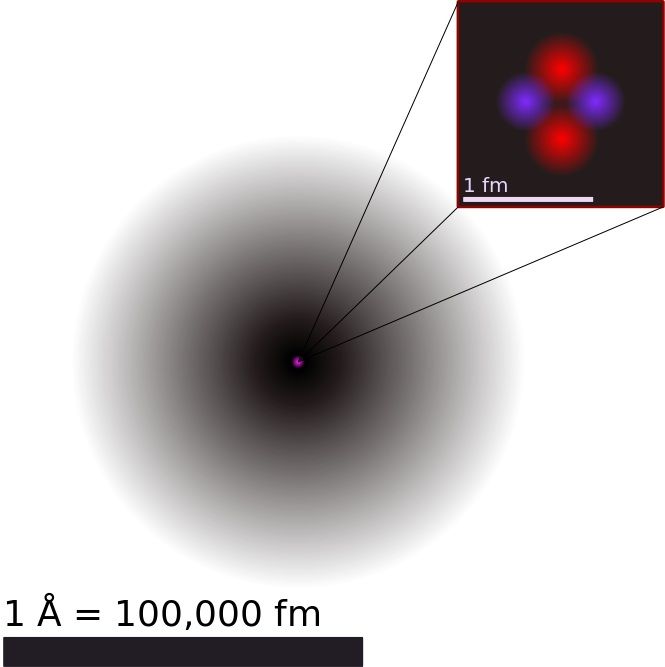
A hullámtermészetnek pedig a Heisenberg-féle határozatlansági reláció a következménye.
Mielőtt megvizsgálunk egy részecskét, az objektum lehetséges állapotát illetően számos valószínűség létezik, de amint megmérjük, a bizonytalanság eltűnik, és a méréssel csak egyetlen állapota lesz a részecskének.

Egy részecske bizonyos értékeit – így például a sebességét és pozícióját – nem tudjuk egyszerre pontosan meghatározni, csak az egyiket lehet pontosan mérni, a másikat már nem. Minél pontosabban meghatározzuk az egyik állapotot, annál pontatlanabbá válik a másik.
Ez a természet egyik alapvető tulajdonsága, amelyet nem lehet kikerülni.
A Heisenberg-féle határozatlansági relációval matematikailag le lehet írni, és oly pontossá tenni a közelítéseket, hogy azok összhangba hozhatók a kísérletekkel, és megfelelnek a tapasztalati tényeknek.

Korábban a newtoni törvények alapján természetesnek vették, hogy a fizikai törvények nem függnek a mérettől, illetve determinisztikusak, de kiderült, hogy a kvantummechanikában ez nem így van.

A részecskék világában uralkodó mikroskála egészen eltér a hétköznapi világunktól, ahol a véletlenszerűség dominál.
De minden látszólagos bizarrsága ellenére, a kvantummechanika is nagyon jól tesztelt.
A kvantumelméletből származó technológiai műszerek, mint például a lézer és a mikrochip, ma már minden számítógép, mobiltelefon és MP3-lejátszó természetes tartozékának számít.
Heisenberg 1925-ben kidolgozta a mátrixmechanikát, Schrödinger pedig egy évvel később, 1926-ban a hullámmechanikát.

Bár a kétféle megközelítés látszólag nagyon eltérő – mátrixegyenletek állnak szemben egy parciális differenciálegyenlettel – Schrödinger megmutatta, hogy ennek ellenére mindkét elmélet egyenértékű.

Őket követve Paul Dirac brit Nobel-díjas fizikus volt az, aki megalkotta a relativisztikus kvantummechanika alapegyenletét, az úgynevezett Dirac-egyenletet, és kidolgozta a kvantummechanika egységes formalizmusát is.
Einstein soha sem érte el élete nagy célját, az egyesített elmélet megalkotását. Neki, és másnak sem sikerült eddig. Az egyesített elmélet az a teória, amely összhangba hozná a relativitás és a kvantumelméletet.

A múlt század folyamán a kutatók három alapvető erőt egyesítettek egyetlen modellbe,
ez a híres „Standard Model”, de a negyedik kölcsönhatást, a gravitációt már nem sikerült beleilleszteniük ebbe. A Standard Modell az univerzum általános működését próbálja meg leírni.

Ebben a modellben lett összefoglalva, hogy a részecskék és a négy alapvető erőből három, az erős, a gyenge és az elektromágneses kölcsönhatás hogyan kapcsolódnak egymáshoz.
Sikeresen megmagyaráz majdnem minden kísérleti eredményt, és pontosan megjósolta a jelenségek széles skáláját.

A természet négy alapvető erője az erős kölcsönhatás (ez tartja össze az atommagban a protonokat és neutronokat, valamint a protonokat és a neutronokat alkotó részecskéket, a kvarkokat, nagyon erős, de csak kis távon hat az atommagban), a gyenge kölcsönhatás (a radioaktiv bomlások közül ez okozza a béta-bomlást), az elektromágneses erő (hatótávolsága akkora mint a gravitációnak, a távolság négyzetével csökken, de csak elektromos töltésű részecskékre hat – a kémiai és biológiai folyamatokban ezek hatnak –) és a gravitációs erő.
A gravitációs erő túlmutat a Standard Modell keretein; az általános relativitás elmélethez tartozik.
A Standard Modell a fentieken kívül magába foglal egy csomó olyan szubatomi objektumot, amelyek csak tiszavirág-életűen léteznek, mint amilyenek a kvarkokból álló részecskék, amelyek nagyon gyorsan elbomlanak, vagy mint az olyan „hétköznapi” részecskék, amelyeket rendkívül nehéz nyomon követni, ilyenek például a neutrínók.
Az általános relativitáselmélet szerint a téridő nyúlik, hajlik, a kvantumelmélet szerint kis skálán pedig minden véletlenszerűvé válik.
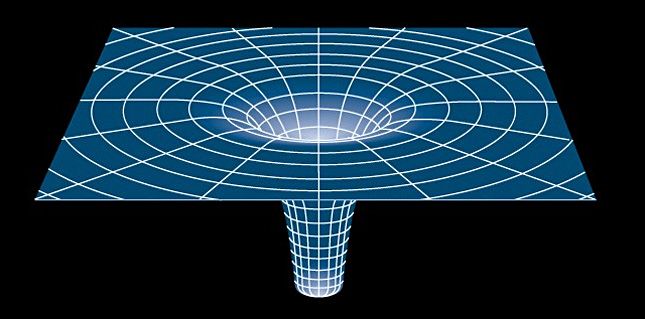
E kettőből együtt az következik, hogy nagyon kis skálán a téridő is véletlenszerűvé válik, majd végül szétszakad.
Mivel valójában nem ez történik, valami nem stimmel a két elmélet kombinációjával.
De mi? Eleinte azt gondoltuk, hogy a természet alap, oszthatatlan építőkockái pontszerűek, de lehet, hogy ez nem szükségszerűen igaz. És itt jön a képbe a húrelmélet.
A húrelmélet azt sugallja, hogy az alapvető építőkockák nem pontok, hanem húrok,
amelyeknek van kiterjedése, azaz hossza. A különböző részecskék és erők ebből a megközelítésből alapvetően olyan húrok, amelyek különböző módok végtelen sokaságában rezegnek.
A húrelmélet mögötti matematika igen hosszú és komplikált, de már részletesen kidolgozott. Azonban ez eddig csak elmélet, mert még senki sem látott ilyen húrokat.

A húrok mérete a számítások szerint 10-34 méter lehet, ez pedig sokkal kisebb, mint amit észlelni tudunk,
még a CERN nagy felbontású műszereivel sem láthatók.
Mégis ez az egyetlen ismert mód a két különböző teória kombinálására. Az elmélet matematikai eleganciája sok tudósnak elegendő ahhoz, hogy kövesse.
Most a fizikusok – a Princeton Egyetem kutatói és volt diákjai – behozták a modellbe a gravitációt is, igaz, nem oly módon, ahogyan azt Einstein elképzelte, és ez a gravitáció nem pont az, amit mi ismerünk,
hanem annak egy kissé „gyűrött” verziója, ami tartalmaz egy extra dimenziót is.
Az általunk ismert univerzum négydimenziós, tér és idő, magasság, mélység, szélesség és az idő együtt alkotja a téridőt.

A legújabb megközelítés szerinti gravitáció leírása ad egy olyan ötödik dimenziót is, ami a téridő görbületét okozza. Az univerzumban meggörbült téridő másolatokat tartalmaz a négydimenziós sima térről, újraskálázva aszerint, hogy hol találhatók az ötödik dimenzióban.

Ennek a furcsa görbült téridőnek a neve Anti-de Sitter (AdS) tér, Einstein munkatársa, Willem de Sitter holland csillagászról elnevezve.

A jelenleg folyó munka olyan utakat is megmutat,
amiben Einstein gravitációs elmélete a fizika más területeihez kapcsolódik.
Ez a felfedezés lehetővé teszi a tudósok számára, hogy egy fizikai ágazatot használjon más látszólag nem kapcsolódó fizikai területek kutatásához.
Igor Klebanovnak, a Princeton Egyetem fizika professzorának voltak sejtései ezen a téren már az 1990-es években. A mostani felfedezés a fizika sok területének metszéspontján fekszik. Az 1970-es években fedezték fel a kvarkokat.
A fizikusok furcsának találták, hogy akármilyen erővel ütköztettek két protont, a kvarkok nem szabadultak fel, hanem a protonba zárva maradtak, ha pedig elszakadtak tőle, akkor rögtön egy antikvarkkal egyesülve mezonná alakultak, így szabad kvarkot soha sem sikerült észlelni.

Alexander Poljakov, a Princeton fizikaprofesszora rájött, hogy a kvarkokat az úgynevezett gluonok tapasztják össze.
Azt feltételezték, hogy a gluonok húrokba rendeződnek, amelyek egymáshoz kötik a kvarkokat, de a részecske- és a húrelmélet közti kapcsolatra nem voltak pontos példák.

A húrelmélet az 1980-as években terjedt el,
ami a részecskéket kis vibráló húrdaraboknak írja le. Ahogy egy rezgő hegedű húr különböző hangokat kelt, minden húr rezgése megjövendöli a részecske tömegét és viselkedését.

Klebanov (Poljakov kollégája) két tanítványával a húrelméletet használta fel ahhoz, hogy kalkulációkat végezzen a gluonokról, aztán a kapott eredményeket összehasonlította a húrelmélettel, hogy ezzel a megközelítéssel megértsen egy fekete lyukat.
A két megközelítés nagyon hasonló választ adott. Egy évvel később Klebanov tanulmányozta a fekete lyuk abszorciós rátáját, és ezúttal
a két megközelítés pontosan megegyező eredményt mutatott.
Ez a munka azonban csak a gluonokra és a fekete lyukakra korlátozódott.

1997-ben Juan Maldacena fizikaprofesszor általánosabb kapcsolatba hozta ezeket az eredményeket. Felfedezett egy összefüggést a gravitáció egy speciális formája és a részecskeelmélet között.

A Princeton kutatói, felismerve Maldacena felismerésének fontosságát,
egy dolgozatban precízebben megfogalmazták Maldacena ötletét,
majd Edward Witten, az Institute of Advanced Study fizikusa ezt tovább fejlesztve írt egy tanulmányt, és e három dolgozat kombinációja hozta el a nagy áttörést.
Ez a kapcsolat azt jelenti, hogy a gravitáció és a szubatomi részecske kölcsönhatásai ugyanannak az éremnek a két oldala. Az egyik az Einstein általános relativitáselméletéből származó gravitáció egy kiterjesztett verziója, a másik pedig a szubatomi részecskék viselkedését és kölcsönhatásait általánosan leíró teória.

Az Asd tér matematikai számításai olyan problémákra is alkalmazhatók, mint a szubatomi részecskék viselkedése az egyesített térelmélet nevű matematikai kapcsolattal leírva, amely
összekapcsolja a négydimenziós részecsketeóriát az ötdimenziós húrelmélettel.
Ez az úgynevezett AdS/CFT (CFT: Conformal Field Theory: egyesített térelmélet) összefüggés. Az AsD/CFT kapcsolatnak sok praktikus felhasználási lehetősége adott.
Például a fekete lyukaknak emelkedik a hőmérséklete, mert minden egyes fekete lyukba hulló részecskének van egy távolható párja, ami hő formájában megmenekülhet a gravitációtól.

Az AdS/CFT módot használva felfedezték a távolható részecskék tanulmányozásának egy új geometriai módját is.
Egy másik példa a káoszelmélet, ami olyan dinamikai rendszerekkel foglalkozik, amelyeket bár determinisztikus törvényszerűségek határoznak meg, mégsem jelezhetők előre, a kvantumkáosz elmélet pedig a kvantumelméletet követő nem determinisztikus rendszerekkel foglalkozik.
A káosz számítása nehéz, de a fekete lyuk segíthet ebben.
A fekete lyuk az egyik legkaotikusabb kvantumrendszer. Maldacena két kollégájával az AdS/CFT módszerrel bemutatták, hogy a fekete lyuk modellezni tudja a kvantumkáoszt. Maldacena reméli, hogy az AdS/CFT összefüggés segítségével hamarosan megtudjuk, hogy milyen lehet a fekete lyuk belül.

Eddig csak arról van képünk, hogy milyen a fekete lyuk kívülről nézve. Maldacena és kollégái úgy vélik, hogy rövidesen megértik a lyukban lévő szingularitást.
Lehetséges, hogy e kapcsolat felismerése feltárja majd a gravitáció kvantumtermészetét is.

Azonban az AdS/CFT a téridő egy egyszerűsített változatára támaszkodik, ami nem teljesen azonos a valós univerzummal.
A kutatók most azon dolgoznak, hogy megtalálják a teória szélesebb körű felhasználásának módszereit
a mindennapi világban, így például a nehéz-ionok ütközéseinél, a nagy hőmérsékletű szupervezetők esetén. Ám a nagy tudományos „Szent Grál” felfedezése, hogy minderre megtalálják az alapvető fizikai elveken alapuló bizonyítékot is, egyelőre még várat magára.












