Lehetséges, hogy a kísérteties távolhatás és a féreglyukak között kapcsolat van

Juan Maldacena és Leonard Susskind fizikusok azzal az ötlettel áltak elő, hogy az összefonódott részecskéket féreglyukak kötik össze. Ez egy merész és radikális feltételezés, mivel ez egy gravitációval összefügő magyarázatot ad (vagyis a féreglyukak) egy kvantummechanikai jelenségre (vagyis az összefonódásra).

A kvantumösszefonódást számos tanulmány vizsgálta, rejtélyes természetük és ígéretes valós világbéli alkalamazásai maitt. Ben Kain, az amerikai, jezsuita  Szent Kereszt Egyetem kutatója nemrégiben bevezetett egy szimuláció alapú modellt, ami felvázolja az összefonódott részecskék és a féreglyukak közötti kapcsolat lehetőségét. - írja a phys.org.

A Physical Review Letters magazinban prezentált modelljével tesztelni és tanulmányozni lehet a Juan Maldacena és Leonard Susskind fizikusok által nemrégiben bemutatott elméleteket. 2019-ben Kain a Dirac csillagokat tanulmányozta.

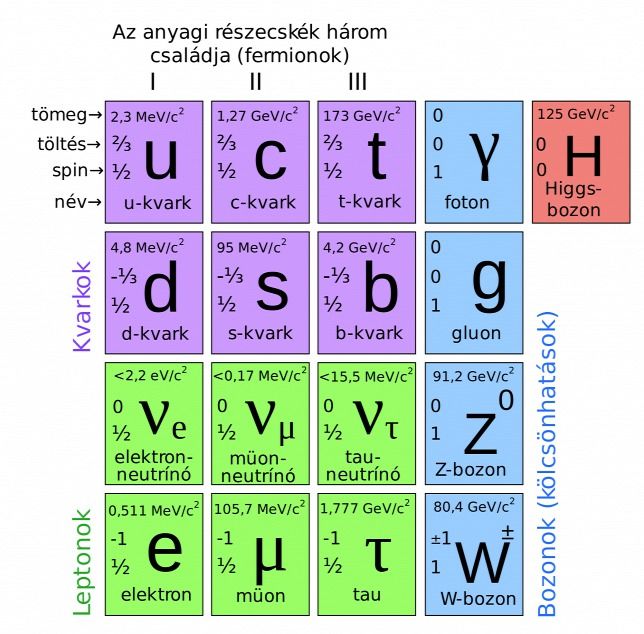
A fermionokat a Dirac-egyenlet írja le, és amikor az általános relativitással párosítjuk, csillagszerű megoldásai vannak, amelyben a fermionok megtartják konfigurációjukat a gravitációs interakciójuk folyamán. A fermionokkal teli csillagok hagyományos leírásai nem teljesen igazolják az általános relativitást.

(A fermionok félspinű szubatomi részecskék, melyek engedelmeskednek a Pauli-féle kizárási elvnek. Ebbe az osztályba tartoznak a szokványos anyagot felépítő részecskék is az elektronok, protonok, neutronok és kvarkok is. A fermionok közvetítő részecskket cserélnek egymással. A Pauli-féle kizárási elv kimondja, hogy egy rendszeren belül két fermion nem lehet azonos kvantumállapotban. A Dirac-egyenlet a Schrödinger-egenlet nem-relativisztikus verziója, ami figyelembe veszi a speciális relativitáselméletet. A szerk. megjegyzése.)

A fermionok félspinű szubatomi részecskék, melyek engedelmeskednek a Pauli-féle kizárási elvnek. Ebbe az osztályba tartoznak a szokványos anyagot felépítő részecskék is az elektronok, protonok, neutronok és kvarkok is. A fermionok közvetítő részecskket cserélnek egymással. Forrás: https://www.vilaglex.hu/Lexikon/Html/Fermion_.htm

Kain két kollégájával korábban írt egy olyan kódot, ami lehetővé teszi a Dirac csillagok szimulációját. Néhány évvel ezelőtt más kutatók felfedezték, hogy amikor ezek a Dirac rendszerek elektromos töltést tartalmaznak, akkor féreglyukakat tartalamznak. A féreglyukak Einstein gravitációs tér egyenleteinek megoldásai. Nemrégi dolgozatok arra utalnak, hogy az elektromos töltésekkel rendelkező Dirac csillagoknak féreglyuk megoldásai vannak, azt feltételezve, hogy a féreglyukak átkelhetők, ami azt jelenti, hogy a részecskék át tudnak haladni az egyik oldalról a másik oldalra. Kain úgy gondolta érdekes lenne, ha szimulálni tudná ezt a féreglyukat és megerősítené, ha átkelhetők. A Dirac rendszer, amire fókuszált Kain, két fermiont fog be. Kain szimulációi azt kívánják, hogy a rendszer gömbszimmetrikus legyen, mivel így könnyebben meg lehet oldani. Ahhoz, hogy gömbszimmetrikus legyen, a rendszer teljes szögmomentuma zéró kell legyen. Ehhez az kell, hogy a két fermion szingulett állapotban legyen, ami összefonja a részecskéket.

Körülbelül egy évtizeddel ezelőtt Maldacena és Susskind azzal az ötlettel ált elő, hogy az összefonódott részecskéket féreglyukak kötik össze. Ez egy merész és radikális feltételezés, mivel ez egy gravitációval összefügő magyarázatot ad (vagyis a féreglyukak) egy kvantummechanikai jelenségre (vagyis az összefonódásra).

Juan Maldacena és Leonard Susskind fizikusok azzal az ötlettel áltak elő, hogy az összefonódott részecskéket féreglyukak kötik össze. Ez egy merész és radikális feltételezés, mivel ez egy gravitációval összefügő magyarázatot ad (vagyis a féreglyukak) egy kvantummechanikai jelenségre (vagyis az összefonódásra). Forrás: https://scienceexchange.caltech.edu/topics/quantum-science-explained/entanglement

Az összefonódás a fénynél gyorsabb kommunikációt igényel, bár ez az ember által nem használható üzenetküldésre. Maldacena és Susskind azt veti fel, hogy a fénynél gyorsabb kommunikáció egy féreglyukon át történhet meg. Azt is sugallják, hogy a féreglyuk nemátszelhető kell legyen (vagyis az emberek nem tudnak átutazni rajta), hogy konzisztens legyen azzal, hogy az emberek nem képesek hasznosítani a rendszert, hogy a fénynél gyorsabban küldjenek üzenetet.
Kain a dolgozatában egy új modellt mutat be, ami segíthet Maldacena és Siskind hipotézisét megvizsgálni. A modell alapja két, egy féreglyuk által összekapcsolt összefonódott fermion szimulácója. A szimuláció működése közben Káin azt találta, hogy hogy ebben a forgatókönyveb a fekete lyukak gyorsan alakulnak ki, eltakarván féreglyuk két végét. Ezek a fekete lyukak végülis a féreglyukat nem átszelhetvé teszik, ami azt jelenti, hogy semmi nem tud áthaladni rajta és elérni a másik végét.Mivel a modell két összefonódott fermion ír le, melyeket egy nem átszelhető féreglyuk kapcsol össze, ez egy konkrét modell Maldacena és Susskind sejtésének tanulmányozására. Maldacena és Susskind a feltételezésüket úgy nevezik: ER=EPR. ER: Einstein-Rosen híd, mert ez első neve volt egy féreglyuknak.

A féregjárat egy csatorna a téribőben, ami összeköti a kozmosz különböző részeit. Forrás: https://www.sciencenews.org/article/black-hole-circling-wormhole-weird-gravitational-waves

EPR: Einstein-Podolsky-Rosen, mert elsőként ők tanulmányoztak összefonódott részecskéket. A modell, amit Kain tanulmányozott így az ER = EPR egy konkrét példája.
Ez az új dolgozat egy új modellt mutat be, ami megvizsgálja a lehetséges kapcsolatot a kvantumösszefonódás és a féreglyukak között. Kain azt reméli, hogy modelljének további vizsgálatával a kutatók képesek lesznek meghatározni, hogy vajon Maldacena és Susskind hipotézise helyes-e, miközben azt is meghatározzák, hogy egy féreglyuk hogy tudná elősegíteni a fénynél gyorsabb kommunikációt, ami az összefonódás kulcsfontosságú feltétele.

(Forrás: https://phys.org/)