Ismeri-e a spagetti titkát? Egy kis konyhai fizika

Komoly fizikai feladványt adott a spagetti

A fizika furcsa világa a konyhában is számtalanszor tetten érhető. Érdekes dolgot figyelhetünk meg főzés közben: ha egy spagettiszálat meghajlítunk, mindig legalább három darabra törik, kettőbe sohasem, ellentétben a fa- vagy műanyag pálcával.

Kifogott a spagetti a kiváló fizikuson

A jelenségre Richard Feynman (1918-1988) a kiváló fizikus figyelt fel, mikor egy barátjával spagettit készítettek. Próbáltak magyarázatot találni a különös jelenségre, de hiába.

Komoly fizikai feladványt adott a spagetti Forrás: Origo

Víz alatt is tördelték a szálakat, hátha másra jutnak

a levegőnél mintegy 820-szor sűrűbb közegben, de itt sem lett más a kísérlet végeredménye. Két óra múlva ott ültek egy széttört spagettihalom közepén, de a sok agyalás, kísérletezés sem fejtette meg a spagetti titkát. Feynman később aztán nem is foglalkozott a kérdéssel.

A Nobel-díj átadás inspirálta a diákot

A választ 1991-ben egy akkor érettségi előtt álló francia diák, Basile Audoy adta meg, aki látta a televízióban, amikor Pierre-Gilles de Gennes francia fizikus átvette a fizikai Nobel-díjat a folyadékkristályokkal kapcsolatos munkájáért.

Pierre-Gilles de Gennes francia Nobel-díjas fizikus Forrás: Thefamouspeople.com

Amikor a legnagyobb tudományos elismeréssel kitüntetett tudósnak a Nobel-díj átvétele után feltették a kérdést, hogy a fizikában milyen további nagy problémákat kell még megoldani, ő – többek között - Feyman spagettiesetét jelölte meg.

Ez felvillanyozta Basile Audoy-t, aki elhatározta, hogy megpróbál végére járni a spagetti rejtélyének.

Érdekes interferencia a spagettiszálban

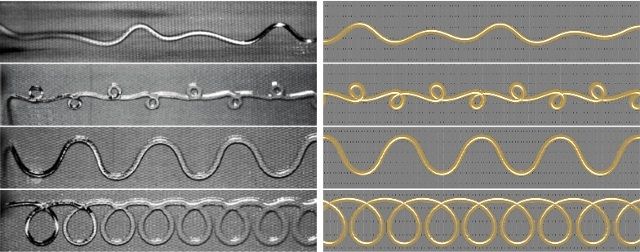
Audoy és kutatótársa, Sébastian Neukirch hatféle spagettivel kísérleteztek. Megfogták egy szál egyik végét, a másikat mozgatták, és nagy sebességű kamerával felvették. A felvételeken látható, hogy a szálon hullámzás fut végig.

Richard Feynman amerikai elméleti fizikus, a spagettiprobléma felfedezője Forrás: Wikimedia Commons

Amikor eltörjük a szálat, az egyik vége a kezünkben van, a másik szabadon.

A szabad vég ki akar egyenesedni, és a görbület energiahullámokat küld végig a tésztaszálon

a kezünk felé, majd onnan visszaverődik, és találkozik a szembejövő hullámokkal. Ilyenkor interferencia keletkezik: ha ellentétes fázisú hullámok találkoznak, kioltják, ha azonos fázisúak, akkor erősítik egymást, utóbbi esetben a görbület megugrik, és a spagetti eltörik.

Basile Audoy (a kép jobb szélén) és kutatótársa, Sébastian Neukirch Forrás: Improbable Research » Blog Archive

A fragmenált darabok görbülete, a törést megelőző görbület 1,5-szeresére növekedhet, és ettől újabb törés keletkezik.

Ha a kezdeti hajlítás egyenletes, az első töréspont a legtökéletlenebb helyen következik be. Amikor egy meghajlított pálca eléri a törési görbületet, eltörik az első pontban, és hullámok törnek ki, futnak végig rajta.

A spagettieffektus Forrás: Columbia.edu

A töréssel újabb görbülethullámok keletkeznek, és a folyamat addig tart, míg az energia annyira lecsökken, hogy a hullám már nem tud végighaladni a spagettiszálon. Számítógépes szimulációval is ugyanerre az eredményre jutottak. Az adatelemzések szerint a törés helye független a szál hosszától, és az elengedéstől eltelt idő négyzetgyökének hányadosa állandó.

A szétesés folyamatának különleges mikrokozmosza

Többnyire csak 1-3 törés jön létre,

bár a modell szerint többnek kéne lennie,

aminek az oka, hogy ha nem tökéletesen fogjuk be a spagetti végét, akkor annak a hossza mentén nem állandó görbület keletkezik.

Ki hinné, hogy milyen komoly fizikai feladványt adott a spagettifőzés? Forrás: Ács Bori

A tudomány és a technika területén sok esetben lényeges a szétesés folyamatának ismerete.

Egy test szilárd darabokra esésekor különböző fizikai jelenségek működnek, melyeket főleg statisztikai szempontból tanulmányoztak, de egyre több munkában benne foglaltatnak a fizikai tényezők is, így például a felületi energia, a rugalmas görbítés, a nyomáshullám-szaporodás, a törési folyamat gócképződésének és növekedésének a szabályszerűsége.

A fizika nemcsak elméleti tudomány, hanem jelen van a mindennapok pillanataiban is Forrás: Youtube

Ha egy kritikus szögnél jobban meghajlítunk egy vékony és törékeny pálcikát, bármi is az anyaga, eltörik, ez az úgynevezett törési görbület. Egy fapálcika vagy műanyag pálcika, kettétörik, de nem úgy, mint a spagetti.