III. Néhány ma is megoldatlan probléma
A három klasszikus geometriai probléma tehát a 19. század végére megoldódott. De a régi görögök több olyan problémát is ránk hagyományoztak, amelyet még ma sem tudunk megoldani. Két ilyen probléma az ún. tökéletes számokkal kapcsolatos. A tökéletes szám definícióját Euklidésznél találjuk: egy szám tökéletes, ha egyenlő az osztói összegével. (A számot magát nem számítva az osztók közé, de az 1-et igen.) Így pl. 6=1+2+3 vagy 28=1+2+4+7+14. Euklidész receptet is ad a tökéletes számok konstrukciójára (IX. könyv 36. tétel): "Ha az egységtől kezdve kétszeres arányban képezünk egy mértani sorozatot, amíg a sorösszeg prím nem lesz, és az összeggel megszorozzuk az utolsó tagot, akkor a szorzat tökéletes szám lesz." Mai jelöléssel ez azt jelenti, hogy
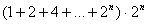

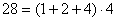
A másik alapvető kérdés Euklidész algoritmusával kapcsolatban az, hogy hány tökéletes számot kaphatunk meg ilyen módon? Azaz: hány páros tökéletes szám van? Vajon végtelen sok van-e, vagy a tökéletes számok sorozata egy ponton véget ér? A tökéletes számok vadászata 2300 éve folyik. Mivel csak Euklidész receptje áll a rendelkezésükre, ezért a matematikusok

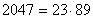
Minden jel arra mutat, hogy a Mersenne-prímek sorozata (és így a páros tökéletes számok sorozata is) végtelen, e tény bizonyítása azonban meghaladja a jelenlegi tudásunkat. Sokan ezt a kérdést olyan reménytelennek tartják, hogy úgy fogalmaznak: az emberiség talán sohasem fogja megtudni, hogy van-e végtelen sok tökéletes szám vagy nincs. Persze ezekkel a jóslatokkal csínján kell bánni.
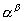
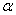
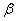
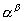
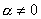
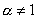
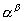
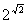


Vastagbélrák szűrése: kiderült, mennyire hatékony a vérteszt

Andrei Mangra botránya folytatódik: egy boltban is balhézott a táncos

"Döntöttem" - Életreszóló döntést hozott Epres Panni, rengetegen támogatják benne

Háború Ukrajnában - Ledobták az elefánt nevű bombát az oroszok + videó

IQ teszt: csak a zsenik jönnek rá, hogy melyik ablak a nagyobb

Újabb megdöbbentő lépés Bidenéktől: nemcsak a világháborút robbanthatják ki, milliárdokat is kaszálhatnak

Miss Universe: nem kímélik a győztes nőt

Pénteki sportműsor: ellenfelet kap a magyar válogatott az NL-osztályozóban; pályán a Bayern és a PSG

Látványos felvétel, így törtek össze az autók az M6-oson a brutális tömegbalesetben - videó

Kerek fenék, csodamellek: felfedezésre vár a bombázó röpis

Mutatjuk, hol kell előkészíteni a hólapátot, több centi hó is eshet


